Cours particuliers de Mathématiques à 69210-lentilly.
Trouvez votre professeur à domicile
7 Professeurs

Emeline
+ 1 matière
- Mathématiques
- Français
Premier cours offert
Mathématiques
- Primaire
- CP 28,50€
- CE1 28,50€
- CE2 28,50€
- CM1 28,50€
- CM2 28,50€
- Collège
- 6ème 28,50€
- 5ème 28,50€
- 4ème 28,50€
- 3ème 28,50€
- Aide aux devoirs 28,50€
- Lycée
- 2de 28,50€
- 2de pro 28,50€
- CAP 28,50€
- BEP 28,50€
Français
- Primaire
- CP 28,50€
- CE1 28,50€
- CE2 28,50€
- CM1 28,50€
- CM2 28,50€
- Collège
- 6ème 28,50€
- 5ème 28,50€
- 4ème 28,50€
- 3ème 28,50€
- Aide aux devoirs 28,50€

Guillaume
+ 1 matière
- Mathématiques
- Mécanique
Premier cours offert
Mathématiques
- Collège
- 6ème 24,00€
- 5ème 24,00€
- 4ème 24,00€
- 3ème 24,00€
- Aide aux devoirs 24,00€
- Lycée
- 2de 24,00€
- 2de pro 24,00€
- 1ère 24,00€
- Term 24,00€
- CAP 24,00€
- BEP 24,00€
- 1ère Pro 24,00€
- Term Pro 24,00€
Mécanique
- Lycée
- 2de 24,00€
- 2de pro 24,00€
- 1ère 24,00€
- Term 24,00€
- CAP 24,00€
- BEP 24,00€
- 1ère Pro 24,00€
- Term Pro 24,00€

Cyril
+ 0 matière
- Mathématiques
Premier cours offert
Mathématiques
- Primaire
- CP 28,50€
- CE1 28,50€
- CE2 28,50€
- CM1 28,50€
- CM2 28,50€
- Collège
- 6ème 28,50€
- 5ème 28,50€
- 4ème 28,50€
- 3ème 28,50€
- Aide aux devoirs 28,50€
- Lycée
- 2de 28,50€
- 2de pro 28,50€
- 1ère 28,50€
- Term 28,50€
- CAP 28,50€
- BEP 28,50€
- 1ère Pro 28,50€
- Term Pro 28,50€

Ademola
+ 0 matière
- Mathématiques
Premier cours offert
Mathématiques
- Superieur
- L1 37,50€
- CPGE 1-Prépa 1 37,50€
- Lycée
- 2de 28,50€
- 2de pro 28,50€
- 1ère 28,50€
- Term 37,50€
- CAP 28,50€
- BEP 28,50€
- 1ère Pro 28,50€
- Term Pro 37,50€
- Collège
- 4ème 28,50€
- 3ème 28,50€
- Aide aux devoirs 37,50€
Boubacar
+ 0 matière
- Mathématiques
Mathématiques
- Superieur
- BTS 28,50€
- L1 28,50€
- Lycée
- 2de 28,50€
- 2de pro 28,50€
- 1ère 28,50€
- Term 28,50€
- CAP 28,50€
- BEP 28,50€
- 1ère Pro 28,50€
- Term Pro 28,50€
- Collège
- 6ème 28,50€
- 5ème 28,50€
- 4ème 28,50€
- 3ème 28,50€
- Aide aux devoirs 28,50€
- Primaire
- CP 28,50€
- CE1 28,50€
- CE2 28,50€
- CM1 28,50€
- CM2 28,50€

Franck
+ 1 matière
- Biologie moléculaire
- Mathématiques
Biologie moléculaire
- Lycée
- 2de 37,50€
- 2de pro 37,50€
- 1ère 41,00€
- Term 41,00€
- CAP 37,50€
- BEP 37,50€
- 1ère Pro 37,50€
- Term Pro 37,50€
- Superieur
- BTS 46,00€
- BTSA 46,00€
- Ecole infirmière 46,00€
Mathématiques
- Lycée
- 2de 37,50€
- 2de pro 37,50€
- 1ère 37,50€
- CAP 37,50€
- BEP 37,50€
- 1ère Pro 37,50€
- Term Pro 37,50€

Charles
+ 0 matière
- Mathématiques
Mathématiques
- Primaire
- CP 28,50€
- CE1 28,50€
- CE2 28,50€
- CM1 28,50€
- CM2 28,50€
- Collège
- 6ème 28,50€
- 5ème 28,50€
- 4ème 28,50€
- 3ème 28,50€
- Aide aux devoirs 28,50€
- Lycée
- 2de 31,50€
- 2de pro 31,50€
- 1ère 31,50€
- Term 33,00€
- CAP 31,50€
- BEP 31,50€
- 1ère Pro 31,50€
- Term Pro 31,50€
- Superieur
- L1 37,50€
- M2 37,50€
- CPGE 1-Prépa 1 41,00€

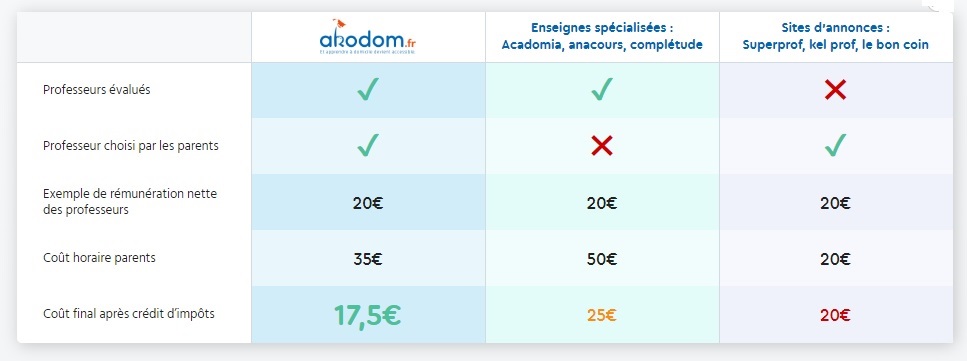
Cours Particuliers à Domicile de Mathématique en 3ème à partir de 12€
Trouvez votre SuperAko-prof de cours de maths
Lors de cette dernière année du collège, les élèves sont confrontés à 2 étapes importantes de leur scolarité :
- Le Brevet des collèges, premier grand examen de leur parcours scolaire
- Leur 1er choix d’orientation
Les mathématiques au Brevet des Collèges
- Le Brevet des Collèges évalue les connaissances et les compétences acquises en fin des années collège.
- Cette évaluation est répartie entre le contrôle continu (400 points) et des épreuves de fin d’année (400 points).
- Le diplôme est obtenu dès lors que l’élève obtient 400 points sur les 800.
- L’ épreuve de mathématiques, d’une durée de 2 heures, permet aux candidats d’obtenir un maximum 100 points.
Les mathématiques en fin de troisième
Les attendus en fin de 3ème concrétisent les 6 compétences majeures en mathématiques développées tout au long du cycle 4 :
1) Chercher
2) Modéliser
3) Représenter
4) Raisonner
5) Calculer
6) Communiquer
Les attendus dans les 5 grands thèmes mathématiques en fin de 3ème
NOMBRES et CALCUL
Utiliser les nombres pour comparer, calculer, et résoudre des problèmes
Nombres
L’élève doit savoir utiliser les puissances d’exposants positifs ou négatifs pour simplifier l’écriture des produits, par exemple 9x9x9x9= ?
Pratiquer le calcul mental, à la main ou avec calculatrice, de manière exacte ou approchée
L’élève doit savoir :
- Calculer avec les nombres rationnels, notamment dans la résolution de problèmes
- Résoudre des problèmes avec des racines carrées
- Résoudre des problèmes avec des puissances, en utilisant la notation scientifique
Comprendre et utiliser les notions de divisibilité et de nombres premiers
L’élève saura :
- Décomposer un nombre entier en produits de facteurs premiers (à la main, avec un tableur ou d’un logiciel de programmation
- Simplifier une fraction pour la rendre irréductible
- Modéliser et résoudre des problèmes faisant appel à la divisibilité
Utiliser le calcul littéral
L’élève sera capable de :
- Déterminer l’opposé d’une expression littérale
- Développer, factoriser, réduire des expressions algébriques simples
- Factoriser une expression du type a²-b² et développer des expressions du type (a+b)(a-b)
- Résoudre algébriquement des équations du 1er degré, des équations produits et des équations de la forme x²=a
- Résoudre des problèmes internes au mathématiques ou lien avec d’autres disciplines
ORGANISATION et GESTION DES DONNEES , FONCTIONS
Interpréter, représenter et traiter des données
L’élève pourra :
- Lire, interpréter et représenter sous forme d’histogramme
- Calculer et interpréter l’étendue d’une série présentée sous forme de données brutes, d’un tableau, de diagrammes
- Calculer des effectifs et des fréquences
Comprendre et utiliser des notions élémentaires de probabilités
L’élève saura :
- Calculer des probabilités, à partir de dénombrement, pour des expériences aléatoires simples à une ou deux épreuves
- Faire le lien entre stabilisation des fréquences et probabilités
Résoudre des problèmes de proportionnalités
L’élève arrivera à :
- Modéliser une situation de proportionnalité à l’aide d’une fonction linéaire
- Faire le lien entre pourcentage d’évolution et coefficient multiplicateur
- Résoudre des problèmes utilisant la proportionnalité dans le cadre de la géométrie
Comprendre et utiliser la notion de fonction
- Utiliser les notations et le vocabulaire fonctionnel
- Passer d’un mode de représentation d’une fonction à un autre
- Déterminer, à partir de tous les modes de représentation, l’image d’un nombre
- Déterminer un antécédent à partir d’une représentation graphique ou d’un tableau de valeurs d’une fonction
- Déterminer de manière algébrique l’antécédent par une fonction, dans des équations du 1er degré
- Représenter graphiquement une fonction linéaire, et affine
- Interpréter les paramètres d’une fonction affine suivant l’aspect de sa courbe représentative
- Modéliser un phénomène continu par une fonction
- Modéliser une situation de proportionnalité avec une fonction linéaire
- Résoudre des problèmes modélisés par des fonctions en utilisant plusieurs modes de représentation
GRANDEURS et MESURES
Calculer avec des grandeurs mesurables et exprimer les résultats dans les unités adaptées
- Calculer le volume d’une boule
- Calculer les volumes d’assemblages de solides étudiés au cours du cycle 4
- Résoudre des problèmes utilisant les conversions d’unités sur des grandeurs composées
- Vérifier la cohérence des résultats du point de vue des unités pour les calculs de grandeurs simples ou composées
Comprendre l’effet de quelques transformations sur les figures géométriques
- Calculer des grandeurs géométriques (longueurs, aires, volumes) en utilisant les transformations (symétries, rotations, translations et homothétie)
- Résoudre des problèmes en utilisant la proportionnalité en géométrie (agrandissement, réduction, triangles semblables, homothétie)
ESPACE et GEOMETRIE
L’élève saura
Représenter l’espace
- Se repérer sur une sphère (type globe terrestre) en identifiant latitude et longitude
- Construire et mettre en relation différentes représentations des solides étudiés au cours du cycle
Utiliser les notions de géométrie plane pour démontrer
- Transformer une figure par rotation et homothétie, en utilisant :
- le théorème de THALES et sa réciproque
- Les triangles semblables (une définition et une propriété caractéristique
- Les lignes trigonométriques dans le triangle rectangle (cosinus, sinus, tangente)
- Identifier des rotations et des homothéties dans des frises, des pavages
- Mobiliser ses connaissances des figures, des configurations, de la rotation et de l’homothétie pour déterminer des grandeurs géométriques
- Mener des raisonnements en utilisant des propriétés des figures des configurations
ALGORITHMIQUE et PROGRAMMATION
Ecrire, mettre au point, exécuter un programme, les 3 niveaux sont attendus en fin de 3ème
- Niveau 1
- Mettre en ordre/ compléter des blocs fournis par l’enseignant afin de construire un programme simple
- Ecrire un script de déplacement ou de construction utilisant des instructions conditionnelles et/ou la boucle « répéter .. fois)
- Niveau 2
- Gérer le déclenchement d’un script en réponse à un évènement
- Ecrire une séquence d’instructions (si …alors, répéter… fois)
- Intégrer une variable dans un programme de déplacement, de construction géométrique ou de calcul
- Niveau 3
- Décomposer un problème en sous problèmes afin de créer des blocs personnalisés
- Construire une figure en créant un motif se reproduisant à l’aide d’une boucle
- Ecrire plusieurs scripts fonctionnant en parallèle pour gérer des interactions et créer des jeux
Source Eduscol 2019
